وقتی یک شبکه طراحی میکنیم، همیشه باید بدانیم که در این شبکه به چند آدرس نیاز داریم. همچنین میخواهیم Range آدرسهای IP شبکه خود را بدانیم تا بتوانیم برای هر دستگاه در شبکه یک آیپی اختصاص دهیم. در این مطلب، قصد داریم یک روش ساده برای یافتن range آدرسهای IP از طریق subnet mask را نشان دهیم.
در IPv4، آدرس IP از عدد ۳۲ بیتی تشکیل شده است و ما آن را با ۴ اکتت یا octet (هر کدام ۸ بیت) نشان میدهیم. معمولا وقتی حرف از شبکه میزنیم به یک سابنت (subnet) هم اشاره میکنیم که میتواند یک عدد باشد (مثلا ۲۴/) و میتوان آن را مانند یک آدرس IP هم نوشت (مثال ۲۵۵.۲۵۵.۲۵۵.۰/). از طریق سابنت، میخواهیم بفهمیم که آدرسهای IP در این شبکه چیست.
به عنوان مثال، اگر یک شبکه ۱۹۲.۱۶۸.۰.۱/۲۴ (یا با سابنت ۲۵۵.۲۵۵.۲۵۵.۰) داشته باشیم، در این صورت ۲۵۶ آدرس قابل استفاده از ۱۹۲.۱۶۸.۰.۰ تا ۱۹۲.۱۶۸.۰.۲۵۵ داریم.
ایده الگوریتم
به طور کلی، اگر ما با آدرس IP به عنوان یک عدد ۳۲ بیتی برخورد کنیم و subnet mask را x داشته باشیم، آنگاه subnet mask از نظر تئوری میتواند مقادیری بین [۳۲، ۰] بگیرد و ما باید دو چیز را تخمین بزنیم، تعداد آدرسهای ممکن با subnet mask داده شده و آدرس شروع.
با فرمول ۲ به توان (۳۲-x) میتوانیم به راحتی تعداد آدرسهای ممکن را به دست آوریم. این بدان معناست که اگر subnet mask صفر داشته باشیم، آدرسهای ممکن ۲ به توان ۳۲ هستند و اگر subnet mask را ۳۲ داشته باشیم، تعداد آدرسهای ممکن ۲ به توان صفر (یک)است، یعنی آدرس داده شده تنها آدرس ممکن در این مورد است. یک مثال دیگر در مورد subnet mask مثلا ۲۴/ را در نظر بگیریم ، ۲ به توان (۲۴-۳۲) که میشود ۲ به توان ۸ و برابر با ۲۵۶ آدرس خواهیم داشت.
بعد باید این subnet mask را به شکل octets تفسیر کرد. اگر subnetmask ما ۲۴/ باشد، در واقع یک عدد ۳۲ بیتی داریم که بیشترین ۲۴ بیت را به عنوان یک دارد و بقیه صفر هستند:

از جدول قبلی، ببینیم که چگونه subnet mask را میتوان تفسیر کرد، اگر یک آدرس IP مانند ۱۹۲.۱۶۸.۰.۱۰/۲۴ داشته باشیم، میتوانیم آن را در جدول بنویسیم تا با اکتتهای باینری مقایسه شود:

آدرس شروع Subnet
برای پیدا کردن آدرس شروع در سابنت زیر، کافیست به سادگی عملیات and باینری را بین آدرس IP و subnet mask انجام دهیم:

آخرین آدرس Subnet
در نهایت، آخرین آدرس IP را با اعمال عملیات or روی آن با معکوس باینری بیتی subnet mask به آدرس IP اول محاسبه میکنیم:
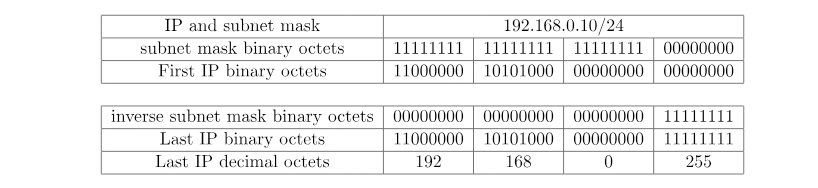
با این مراحل ساده، میدانیم که چگونه تعداد آدرسهای IP ممکن را پیدا کنیم، همچنین میتوانیم اولین و آخرین آدرس IP را پیدا کنیم و محدوده (Range) از ۱۹۲.۱۶۸.۰.۰ تا ۱۹۲.۱۶۸.۰.۲۵۵ میشود.
مثالها:
اگر subnet mask داشته باشیم که دقیقا در یکی از اکتتها نباشد، همین ایده اتفاق میافتد. بیایید نمونه ۱۹۲.۱۶۸.۰.۱۰/۳۰ را ببینیم. با پیروی از همین ایده، ۲ به توان ۲ یعنی ۴ آدرس IP ممکن داریم:
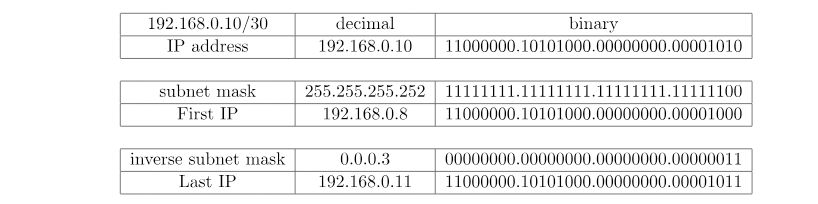
یک مثال دیگر را در نظر بگیریم که در آن subnet mask در اکتت آخر مانند ۱۰.۰.۰.۰/۲۰ نیست. در این مورد ما ۲ به توان (۳۲-۲۰)یعنی ۲ به توان ۱۲ که میشود ۴۰۹۶ آدرس IP ممکن داریم:
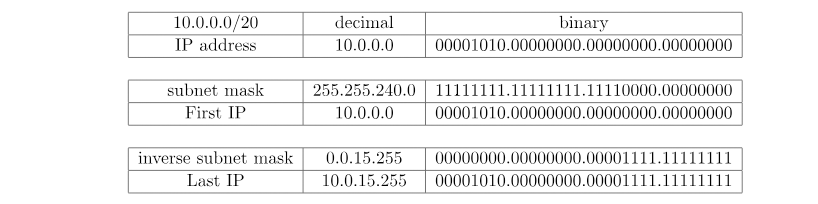
خوشبختانه، در بیشتر زبانهای برنامه نویسی، برای انجام عملیات باینری نیازی به تبدیل بین باینری و دسیمال نداریم. بنابراین، میتوانیم عملیات باینری را مستقیم روی اکثر اعداد قابل شمارش (مانند اعداد صحیح یا کاراکترها) اعمال کنیم. به عبارت دیگر، میتوان آدرس IP را با یک عدد ۳۲ بیتی یا با استفاده از ۴ رقم هر کدام ۸ بیت (مانند کاراکترها یا بایتها) نشان داد.
سرور مجازی امکاناتی همچون کنسول تحت وب، تغییر سیستم عامل، تهیه اسنپ شات، بک آپ و … به صورت فارسی در اختیار شما میگذارد.
خرید سرور مجازی در پنج موقعیت جغرافیایی ایران، ترکیه، هلند، آلمان و آمریکا با قابلیت تحویل آنی در پارسدو فراهم است.
IPv6
در IPv6، همان ایده subnet مشابه IPv4 است. اما تفاوت در اندازه آدرس و محدوده (Range) مجاز است. آدرس IPv6 دارای ۱۲۸ بیت در مقایسه با ۳۲ بیت در IPv4 است. آدرس در ۸ بخش در مقایسه با ۴ اکتت در IPv4 نشان داده شده است. هر بخش دارای ۴ عدد هگز (hex) است که از ۰ تا FFFF در مقایسه با ۸ بیت در هر اکتت در IPv4 با دامنه دسیمال ۰ تا ۲۵۵ استفاده میکند.
به طور کلی، میتوانیم تعداد آدرسهای IP موجود را به همان روشی که در IPv4 انجام دادیم، به دست آوریم. بنابراین، اگر یک subnet به اندازه x داشته باشیم، ۲ به توان (۱۲۸-x) آدرس IP موجود داریم که با اعمال بیتی و با ماسکی به اندازه ۱۲۸ بیت میتوانیم اولین آنها را محاسبه کنیم که x بیتهای اول یک و بقیه صفر هستند و با اضافه کردن اولین آدرس به معکوس ماسک (۱۲۸ بیت با بیتهای x اول صفر و بقیه یک هستند) میتوانیم آخرین آدرس را به دست آوریم.
بیایید یک مثال IPv6 برای ۲۰۰۱ : 124A : 2000 : 1000 : 0000 : 0000 : 0000 : 0000 /48 ببینیم. توجه داشته باشید که هر بخش به صورت ۴ رقم هگز نوشته شده است که برابر با ۱۶ بیت باینری است. تعداد آدرسها ۲ به توان (۱۲۸-۴۸) یعنی ۲ به توان ۸۰ خواهد بود:

توجه داشته باشید که FFFF معادل ۱۶ یک است ۱۱۱۱۱۱۱۱۱۱۱۱۱۱۱۱. نکته دیگر این است که آدرس IPv6 همچنین میتواند با حذف صفرهای ابتدایی در هر بخش، اشکال کوتاه داشته باشد.
بنابراین، آدرس اول مثال خود را می نویسیم:
۲۰۰۱ : 124A : 2000 : 0 : 0 : 0 : 0
و شکل کوتاه شده دیگر این است که یکی از دنبالههای سگمنتهای خالی (همه segmentهای صفر) را با double colon جایگزین کنید. بنابراین، شکل کوتاه شده دیگر این آدرس می شود:
۲۰۰۱ : 124A : 2000 ::
توجه داشته باشید که نسخه کوتاه شده بیش از یک بار اجازه حذف بخشهای صفر را نمیدهد. بنابراین، اگر داریم :
۲۰۰۱ : 124A : 2000 : 0000 : 0000 : 1234 :0000 :0000
نسخه کوتاه شده به صورت زیر خواهد بود:
۲۰۰۱ : 124A : 2000 : : 1234 : 0 : 0
یا:
۲۰۰۱ : 124A : 2000 : 0 : ۰ : ۱۲۳۴ ::
در این نسخه کوتاه شده، میتوانیم بدانیم چند صفر حذف شدهاند، زیرا میدانیم که ۱۲۸ بیت داریم که به ۸ بخش تقسیم شدهاند. بنابراین، ما می دانیم که چند بخش از ۸ حذف میشود و اینها صفرهایی هستند که حذف شدهاند.
پیچیدگی
پیچیدگیهای زمانی و مکانی یافتن Range آیپی O(1) است زیرا ما فقط باید سابنت را در فرمولی قرار دهیم تا range را پیدا کنیم.
نتیجه گیری
در این مطلب روش سادهای را برای تخمین Range آدرسهای IP ممکن از زیر طریق subnet mask توضیح دادهایم. حتما نظرات خود را در این باره در بخش نظرات با ما در میان بگذارید.





